[Cipher] AES(Advanced Encryption Standard), Block Cipher Mode

평소에 AES128, AES192, AES256을 구별해서 사용하지 않고 Java Private Key를 활용해서 자주 암호화 로직에 사용하고 있었다.
AES에서 ECB를 사용하는 것은 권장되지 않고 initialization vector 즉 IV를 활용한 CBC를 활용해야 한다 정도만 알고 있었고 보통 CBC Mode에서 AES를 활용해 왔던 것 같다.
하지만 Block Cipher 모드가 많고 각각 모드별로 취약점과 장단점이 존재하기 때문에 정리를 하게 되었고 그 과정에서 고려사항들을 다시 한번 잘 확인하는 계기가 된 것 같다.

AES 란?

AES (Advanced Encryption Standard)는 대칭 키 암호화 알고리즘으로, 데이터를 안전하게 암호화하고 복호화하는 데 사용됨.
AES는 ISO/IEC 18033-3 표준이며 NSA에 의해 1급 비밀에 사용할 수 있도록 승인된 암호화 알고리즘임.
AES는 세 가지 키 길이를 지원 : 128비트, 192비트, 256비트. 이 키 길이는 암호화의 강도를 결정.
당연하게 비트수가 길수록 보안성을 올라가나 프로세스는 증가함.

AES-128 : 128비트 키를 사용하며, 10 라운드의 암호화 과정을 거침.

AES-192 : 192비트 키를 사용하며, 12 라운드의 암호화 과정을 거침.

AES-256 : 256비트 키를 사용하며, 14 라운드의 암호화 과정을 거침.

Java에서는 SecretKey의 길이에 따라서 정의됨.

Block Cipher Mode

block ciphers : 일반 텍스트 블록을 하나의 블록으로 취급하여 동일한 크기의 암호 텍스트 블록을 얻는 데 사용하는 암호화 또는 복호화 방식.

즉 AES 암호화는 고정된 크기의 데이터 블록을 처리하는데, 이때 평문 데이터의 길이가 블록 크기와 일치하지 않을 경우 패딩이 필요함.

패딩은 데이터 블록을 채워 고정된 길이를 유지하는 방식으로, PKCS#7 같은 표준 패딩 방식을 사용하여 블록을 채움.

들어가기 전 CPA와 CCA에 대해서 한번 짚고 가자.

CPA (Chosen Plaintext Attack) : 암호 해독 자가 사용된 암호기에 접근할 수 있어 평문 P를 선택하여 그 평문 P에 해당하는 암호문 C를 얻어 키 K나 평문 P를 추정하여 암호를 해독하는 방법.
CPA에 대한 방어는 암호 시스템이 임의의 선택된 평문에 대해서도 안전하다는 것을 의미.

CCA (Chosen Ciphertext Attack) : 암호 해독 자가 암호 복호기에 접근할 수 있어 암호문 C에 대한 평문 P를 얻어 내 암호를 해독하는 방법.
암호 분석가가 임의로 선택된 암호문과 일치하는 평문으로부터 암호키를 알아내기 위해 시도하는 공격.
당연히 복호화 장치에 접근 가능한 상황에 사용이 가능.

ECB(Electronic Code Block)

출처 : https://www.highgo.ca/2019/08/08/the-difference-in-five-modes-in-the-aes-encryption-algorithm/

ECB(Electronic Code Book)는 가장 간단한 AES 암호화 모드.

이 모드는 동일한 평문 블록에 대해 항상 같은 암호문 블록을 생성.

특히 이미지와 같은 구조화된 데이터에 사용할 경우 안전하지 않음.

ECB 모드는 병렬 처리가 가능하나, 고유한 보안 취약점 때문에 일반적으로 권장되지 않음.

CBC (Cipher Block Chaining)

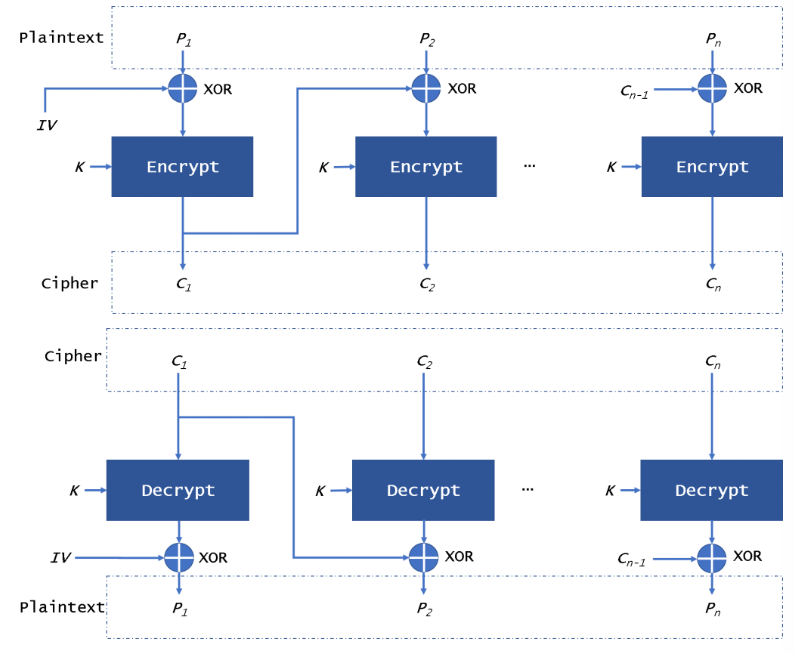
CBC(Cipher Block Chaining) 모드는 initialization vector(IV)를 사용하여 각 블록을 암호화하기 전에 이전 암호문 블록과

XOR 연산.

IV의 주요 목적은 암호화 과정에 무작위성을 추가하여 같은 평문이 같은 암호문으로 변환되는 것을 방지하는 것과 공격자로부터 예측 가능한 패턴을 만들지 않게 하는 것.

XOR 연산
XOR 연산은 암호화 과정에서 중요한 역할을 하며, 키 스트림이나 IV와 평문 데이터를 결합하여 암호문을 생성함
이는 블록의 데이터를 암호화하는 데에 있어서 두 데이터의 비트를 비교하여 같으면 0, 다르면 1을 반환하는 방식으로 작동.

CBC는 같은 평문 블록에 대해서도 다른 암호문 블록을 생성하여 패턴을 숨김.

평문의 길이가 블록 크기의 배수가 아닐 경우, 블록 크기에 맞추기 위해 패딩이 필요.
암호화 과정에서 마지막 블록의 크기가 부족하면, 패딩을 추가하여 블록 크기를 채움.
각 블록이 이전 블록에 의존적이므로, 블록 간의 연관성이 강해짐.
이로 인해 단일 블록의 변경이 전체 암호문에 영향을 미침

그러나, 하나의 블록이 손상될 경우 후속 블록에 영향을 줄 수 있음.

Oracle Padding Attack
Oracle Padding Attack은 암호문의 패딩이 유효한지 알려주는 정보를 이용하는 공격 방식.
암호화된 데이터의 패딩을 검증하는 과정에서 오류 메시지를 통해 유추할 수 있는 정보를 공격자가 수집하고, 이를 이용해 평문을 추론해 내는 방식.
이 공격은 CBC 모드와 같이 패딩이 사용되는 암호화 모드에서 주로 발생할 수 있음.

Oracle Padding Attack 공격과 CCA에 취약할 수 있어, 주기적인 키 교체가 필요함.

2^((n+1)/2)(n은 블록의 길이)를 암호화할 때 키를 변경해야 함.

위 길이 산정의 이유는 바로 아래에서 설명.

CFB (Cipher Feed Back)

1. CFB가 IV를 암호화한 다음 일반 텍스트 블록과 XOR 하여 암호 텍스트를 얻음.
2. 암호화 결과를 일반 텍스트로 암호화.
3. 일반 텍스트를 직접 암호화하지 않기 때문에 암호 텍스트를 사용하여 일반 텍스트와 XOR하여 암호 텍스트를 가져옴.
따라서 이 모드에서는 데이터를 패딩 할 필요가 없음.

XOR 연산하여 암호문을 생성 한 뒤 다음 블록에서는 이전 블록의 암호문 일부를 사용하여 IV로 사용하는 것이 포인트.
평문을 직접 암호화하지 않고, 암호화된 블록(또는 IV)과 평문을 XOR 연산하기 때문에, 평문의 길이가 블록 크기의 배수가 아니어도 블록 크기에 맞출 필요가 없게 돼버림 따라서 패딩이 필요 없음.

또한 암호화가 아닌 병렬로 데이터를 복호화할 수 있음.

이 모드는 CBC와 유사하므로 블록이 깨지면 다음 블록에 모두 영향을 미침.

CFB 모드는 replay attack에 취약함.
이는 CFB가 각 블록의 암호화에 이전 블록의 암호문을 사용하기 때문.
공격자가 암호문의 순서를 변경하거나 재전송함으로써 수신자는 변경된 암호문을 받고, 이를 정상적인 메시지로 잘못 해석할 수 있음.
CBC 모드와는 달리, CFB 모드에서는 단일 블록의 변경이나 재배열이 바로 다음 블록에만 영향을 미치므로, 일부 블록의 재사용이 가능.

CPA로부터는 안전하지만 CCA에 쉽게 노출될 수 있음.

보안을 유지하기 위해 이 모드에서는 2^((n+1)/2) 암호화 블록마다 키를 변경하는 것을 권장함.

왜 2^((n+1)/2) 암호화 블록마다 일까?

https://en.wikipedia.org/wiki/Birthday_problem

Birthday problem - Wikipedia

From Wikipedia, the free encyclopedia Mathematical problem The computed probability of at least two people sharing a birthday versus the number of people In probability theory, the birthday problem asks for the probability that, in a set of n randomly chos

en.wikipedia.org

Birthday Problem.

생일이 366가지이므로 임의의 두 사람의 생일이 같을 확률은 1/366이고, 따라서 366명쯤은 모여야 생일이 같은 경우가 있을 것이라고 생각하기 쉽다.
실제로는 23명만 모여도 생일이 같은 두 사람이 있을 확률이 50%를 넘고, 57명이 모이면 99%를 넘어간다.
이 문제는 무작위로 만난 366명의 생일이 서로 겹치지 않고 고르게 분포할 확률이 사실상 없다는 점을 나타낸다.

암호화 해시 충돌도 역시 같을까?

암호학적 해시 결과 가 같은 두 입력값을 찾는 것 역시 모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시 충돌을 찾을 수 있다.

1. n 비트 값은 이진수로 표현될 때 n 자리를 가지며, 각 자리는 0 또는 1 중 하나의 값을 가질 수 있음.

2. 이와 유사하게, 2비트 값은 00, 01, 10, 11의 4가지 값을 가질 수 있음.

3. 일반화하여, n 비트 값은 2^n개의 고유한 조합을 가질 수 있음.

4. 무작위로 k개의 n 비트 값들을 선택할 때, 각각의 선택은 서로 독립적.

5. 첫 번째 선택은 어떤 2^n 개 중 하나를 선택할 수 있으므로, 충돌 확률은 0.

6. 두 번째 선택에서는 이제 2^n - 1 개의 고유한 값들 중 하나를 선택해야 함.

7. 첫 번째 선택과 동일한 값을 선택하지 않을 확률은 (2^n - 1) / 2^n 이 됨.

8. 이러한 방식으로 계속하면, k 번째 선택에서는 2^n - (k - 1) 개의 고유한 값들 중 하나를 선택해야 하므로
충돌하지 않을 확률은 (2^n - (k - 1)) / 2^n이 됨.

9. 충돌이 발생하지 않을 확률을 모두 곱한 값이 0.5(즉, 충돌 확률이 50%가 되는 지점)에 도달하는 k의 값은 대략 2^(n/2) 임.

10. 즉 n 비트 값들 중 적어도 하나의 쌍이 동일할 확률이 50%에 도달하는 지점을 나타냄.

하지만 실제 충돌이 발생할 가능성이 이론적 확률보다 더 빨리 높아질 수 있다고 가정하는 것이 일반적.

따라서, 2^(n/2) 보다 더 작은 값에서 키를 변경하는 것이 보다 안전하다고 간주됨.

2^((n+1)/2)는 2^(n/2)보다 약간 큰 값이며, 이를 통해 추가적인 보안 마진을 확보하게 됨.

128비트 키: 대략 2.61 x 10^19

192비트 키: 대략 1.12 x 10^29

256비트 키: 대략 4.81 x 10^38

OFB(Output FeedBack)

OFB모드에서는 평문 블록은 암호 알고리즘에 의해 직접 암호화되고 있는 것이 아니라 평문블록과 암호 알고리즘의 출력을 XOR 해서 암호문 블록을 만들어 냄.(물론 맨 처음엔 IV를 활용해서 암호화함.)

스트림 암호화
OFB 모드는 블록 암호를 스트림 암호화기처럼 사용하게 만들어, 데이터를 비트나 바이트 단위로 암호화 및 복호화함.
이 스트림은 평문의 길이에 맞춰서 연속적으로 생성되므로, 평문의 길이가 블록 크기의 배수가 아니어도 문제가 되지 않음.
생성된 키 스트림은 평문과 XOR 연산되어 암호문을 생성.
이 과정에서 평문의 길이에 따라 키 스트림의 필요한 부분만 사용되므로, 블록 크기에 맞춰서 데이터를 채울 필요가 없음.
즉 패딩이 필요하지 않음.

OFB 모드는 CPA (Chosen Plaintext Attack)에는 안전하지만, CCA (Chosen Ciphertext Attack)와 PA (Plaintext Attack)에 취약할 수 있음.

특히, 암호문의 일부를 변경하면 평문도 동일한 방식으로 변경되는 특성 때문에 암호문 조작에 취약.

2^(n+1/2) 암호화 블록마다 키를 변경해야 함.

CTR(Counter)

CTR 모드에서는 Encrypt에 대한 입력 블록, 즉 IV로 Counter 값(Counter, Counter + 1,..., Counter + N - 1)이 사용됨

OFB와 매우 유사하지만 CTR은 IV 대신 매번 암호화할 카운터를 사용함.

따라서 카운터를 직접 얻을 수 있다면 데이터를 병렬로 암호화/복호화할 수 있음.

Mallory(공격자)는 암호문의 일부 비트를 변경하여 평문을 깨뜨릴 수 있음.

2^(n+1/2) 암호화 블록마다 키를 변경해야 함.

Summary

Mode	Advantage	Disadvantage
ECB	간편함. 빠름. 암복호화에서 parallel 을 지원함	plaintext의 중복 데이터가 ciper text에 반영될 수 있음. plaintext가 cipertext를 delete하거나 replace하면서 작동할 가능성이 존재. ciphertext packet 이 손상되었으면 plaintext 에 영향을 줄 수 있음. replay attack 에 취약함, 사용하면 안됨
CBC	parallel computing 을 decryption 단계만 지원.<br> ciphertext packet을 decrypt하는데 빠름. plaintext내에 중복된 데이터가 ciphertext에 반영되지 않음	암호화 과정에서 parallel computing 을 지원하지 않음. 잘못된 block이 이후에 올 block에 영향을 끼칠 수 있음
CFB	padding 을 하지 않음. parallel computing 을 decryption 단계만 지원. ciphertext packet을 decrypt하는데 빠름. 사전에 암호화, 복호화를 prepared 할 수 있음	암호화 과정에서 parallel computing 을 지원하지 않음. replay atttack에 대처가 안됨. 잘못된 block이 이후에 올 block에 영향을 끼칠 수 있음
OFB	padding 을 하지 않음. 암호화. 복호화를 미리 prepared 할 수 있음. 암호화와 복호화에 같은 구조를 사용함. BadBlock은 오직 최신 Block에만 영향을 끼침	parallel computing을 아에 지원안함. Mallory(악의적 공격자)는 몇몇 손상된 ciphertext를 plaintext로 변경할 수 있음
CTR	padding 을 하지 않음. 암호화. 복호화를 미리 prepared 할 수 있음. parallel computing을 지원함. 암호화와 복호화에 같은 구조를 사용함. BadBlock은 오직 최신 Block에만 영향을 끼침	Mallory(악의적 공격자)는 몇몇 손상된 ciphertext를 plaintext로 변경할 수 있음